The board game of Go, or 圍棋 (weiqi), started receiving a lot of attention when
AlphaGo beat the European champion Fan Hui in all of the five games. Now people are worried when AlphaGo is on its way to beat the world champion Lee Sedol, winning
3 out of 5 games so far. AlphaGo plays the game like no human as seen the game played before, inciting the awe of
sadness and beauty. It is touted as an accomplishment of machine intelligence because traditionally the game of Go is very difficult for a machine to play well, whereas games like Chess is well-understood.
Board games are fascinating because a few number of rules allow an exponential number of possible game moves, some with winning outcomes, and some with losing. Traditionally, a naive game solver for any game tries all the possible positions of each alternate side's game play some number of steps ahead and chooses the first move that leads to the best gameplay after that number of steps, known as the
min-max algorithm. Pruning heuristics is applied to reduce the search space so the computer does not waste time searching down "lost cause" paths, known as
alpha-beta pruning. Even with pruning, the search space is still exponential to the number of positions on the board.
The keyword here is exponential. The machine can spend more time to compute, but for the amount of time spent \( t \), it can only search by \( \log{t} \) more steps. We can attempt to parallelize exponential search by enlisting the help of some number of machines, but it will still only allow us to advance the search depth by \( \log{n} \), i.e. the added intelligence is logarithmic to the number of machines.
Chess is well-understood. The number of game play combinations are vast, but we have found ways to prune the search space so that it is tractable with computer clusters that are practical to build. Computers can beat human playing Go on a smaller \( 9 \times 9 \) board with an upper bound of \( (9 \times 9)! \) or \( 10^{121} \) possible game plays, but on a professional championship level, the board size \( 19 \times 19 \) sports an exponential explosion of an upper bound of \( (19 \times 19)! \) or approximately \( 10^{768} \) possible game plays.
Even though Google might undertake the most ambitious of data center builds, they couldn't possibly shut down all the kitten videos on YouTube so AlphaGo could play against Lee Sedol with super-intelligence. Even so, they would achieve only logarithmic increase in intelligence. Building machines to brute force an exponential algorithm is a sure way to go bankrupt (NSA is an exception because the government prints the money).
I feel that a disclaimer is in order before I write any further. I don't have insider knowledge about how AlphaGo works. Everything I'm about to speculate comes from common sense and public sources.
AlphaGo algorithm reduces the search space using
Monte-Carlo tree search, which means it randomly prunes some moves to reduce the branching factor, which allows the search to go deeper. The pruning is guided by deep neural network so it decreases the probability of pruning winning moves. Deep neural network works by building a hierarchy of signal processing nodes that amplifies certain signals after training.
When using DNN to recognize pictures, we can visualize how it works by
looking at the images synthesized iteratively in order to boost certain signals.
In computer science, a pervasive strategy to design a super-efficient algorithm is by
divide and conquer: basically, a big problem is solved by breaking down the problem into smaller sub-problems, until the problem becomes trivially solvable. Here are some examples:
- Sorting is taught to every first year computer science undergraduate. Given \( n \) items to sort, a naive sorting algorithm like bubble sort will take \( O(n^2) \) steps, whereas better ones using divide and conquer like quick sort or merge sort will take \( O(n \lg{n}) \) steps. If we are to sort 1000 items, this makes the difference between 1 million steps verses just 10000 steps.
- First year graduate student would likely learn about discrete Fourier transform. A naive DFT takes \( O(n^2) \) steps, whereas fast Fourier transform using divide and conquer takes \( O(n \lg{n}) \) steps.
- A naive matrix multiplication takes \( O(n^3) \) steps for an \( n \times n \) matrix, but Strassen's algorithm using divide and conquer takes \( O(n^{\lg{7}}) \) or approximately \( O(n^{2.8}) \) steps.
- The n-th Fibonacci number can be computed in \( O(\lg{n}) \) time using a divide and conquer method. The straightforward iterative method would take \( O(n) \) time, and a naive recursive method would take \( O(2^n) \) time. See Fibonacci Number Program for some examples in code.
For other algorithms, divide and conquer may not reduce the number of steps, but it still improves computation performance due to better cache locality. Divide and conquer is the basic idea of
cache oblivious algorithms.
In other words, the real innovation of AlphaGo is not because machines achieved singularity, but because deep neural network approximated the divide and conquer method which happens to allow Go to be played efficiently.
The outcome of Go is scored by determining whether the pieces can survive locally, and the territorial occupation by the surviving pieces. This makes the winning strategy two-fold: on one hand, a player needs to ensure local survival of the pieces, but he has to take the territory into account. If a local battle is losing, it could be better for a player to strengthen his position on a different part of the board. This division of local and global thinking lends itself very well to using the divide and conquer method.
Here are some ideas how to divide. On the first level, we divide the board into subregions of \( 10 \times 10 \) each (figure left). We can also add overlapping subregions of \( 9 \times 9 \) or \( 9 \times 10 \) (figure right). This results in the first level division into \( 3 \times 3 \) subregions.
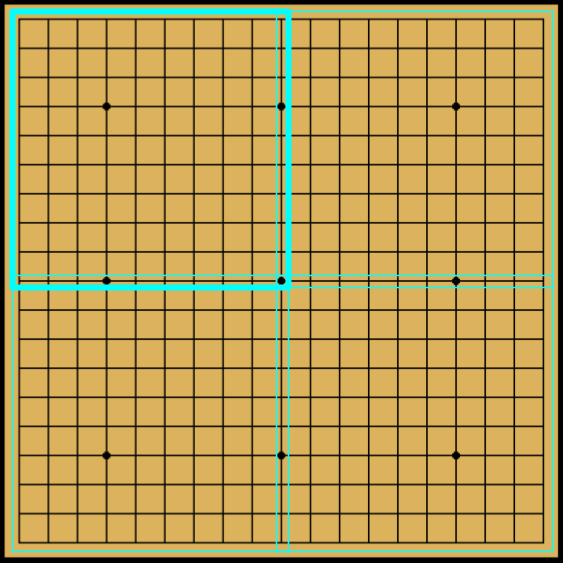 |
| Left: Level 1 |
|
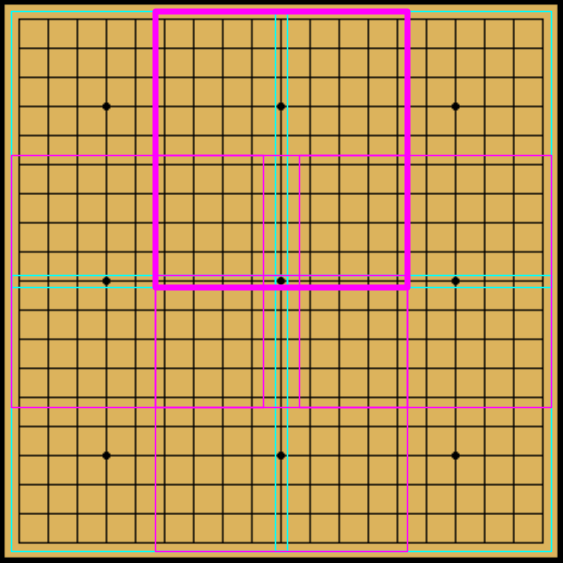 |
| Right: Level 1 overlaps |
|
Each subregion can be divided further into \( 5 \times 5 \) or \( 5 \times 4 \) grids with overlaps. In the following figure, only the division of the first subregion is shown, but it should be understood that the same division will take place for all first level subregions.
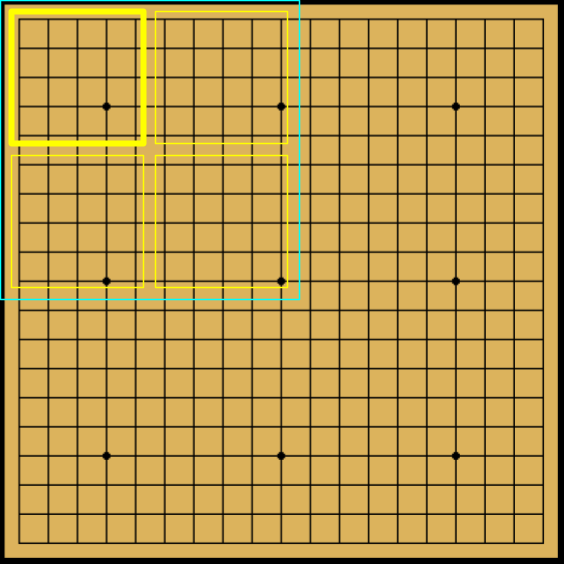 |
| Left: Level 2 |
|
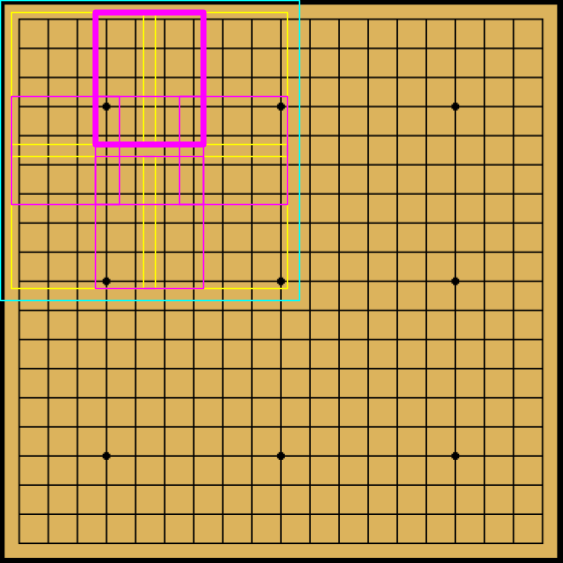 |
| Right: Level 2 overlaps |
|
A sketch of the divide and conquer algorithm would play Go by first choosing the region to play by valuation of the amount of territory it can likely occupy. Then within each region, it could brute force the positions that maximizes the survival of its own pieces.
Here is a very rough guesstimate of the number of steps needed to solve the game. These moves can be grouped into streaks of local battles taking place in \( 3 \times 3 \) subregions, and each streak is further divided to settle the \( 3 \times 3 \) sub-subregions which are about \( 5 \times 5 \) by grid. This reduces the amount of search space to be just:
\[ (5 \times 5)! \cdot (3 \times 3)! \cdot (3 \times 3)! \approx 10^{36} \]
This is a lot more computationally tractable. Of course, the caveat of my calculations is that I have never implemented a divide and conquer player for Go, and I don't know how well it works in practice. But even if we have to add a few levels of \( 3 \times 3 \) division, multiplying the search space by \( 9! \) still grows a lot slower than the exponential explosion of \( (9 \times 9)! \).
\[ (5 \times 5)! \cdot (9!)^9 \approx 10^{75} \]
Using this divide and conquer method, we can envision a game of Go played on a much bigger board, maybe like the
3-dimensional chess depicted in Star Trek.
The difference between the world champion Go player such as Lee Sedol and a modest Go player who happens to be a computer scientist, is that a computer scientist understands the power of divide and conquer. There is an immense beauty of divide and conquer that reaches far beyond game play. Nobody is worried when a computer doing quick sort can sort numbers faster than a human can with no sorting strategy, so why should we worry that a computer using divide and conquer can play a board game better than humans with only an ad-hoc strategy?
No, the computer is not about to achieve singularity. It is just a tool that helped us understand the game better.

